TheanoでLSTM②
前回の続き
kento1109.hatenablog.com
今回はLSTM層の構築から見ていく。
lstm_layer
nsteps = state_below.shape[0] if state_below.ndim == 3: n_samples = state_below.shape[1] else: n_samples = 1
state_belowは、emb、
つまり、nstepsは、文書の長さ
※全文書が事前に固定の長さに合わせられている。
次のifは、Trueが想定されるので、
n_samplesは、バッチサイズ(文書サンプル数)となる。
次の関数は一旦、飛ばして
state_below = (tensor.dot(state_below, tparams[_p(prefix, 'W')]) + tparams[_p(prefix, 'b')])
これがとてもややこしかった。
でも、ここは入力層→隠れ層の大事な部分。
まぁ、自分なりの解釈で進める。
state_below:3階テンソル(文書の長さ×文書サンプル数×128)
まず、state_belowに渡される embについて整理する。
embは、
emb = tparams['Wemb'][x.flatten()].reshape([n_timesteps, n_samples, options['dim_proj']])
で定義されていた。
tparams['Wemb']は、10000×128の行列、
xは、文書の長さ×サンプル数の行列
xをflatten()で一次元するとこんな感じになる。
| doc1,seq1 | doc2,seq1 | ... | docn,seq1 | doc1,seq2 | doc2,seq2 | ... | docn,seqn |
そのベクトルをtparams['Wemb']から抽出する。
イメージはこんな感じ。
import numpy as np vocab = 10 dims = 5 emd = np.random.rand(vocab, dims) target = np.array([[1, 3], [2, 6], [0, 5]]) print target.flatten() [1 3 2 6 0 5] print emd[target.flatten()] [[ 0.528 0.989 0.328 0.764 0.772] # embeddings of word 1 [ 0.719 0.04 0.249 0.537 0.021] # embeddings of word 3 [ 0.919 0.415 0.88 0.175 0.197] # embeddings of word 2 [ 0.622 0.713 0.354 0.063 0.126] # embeddings of word 6 [ 0.171 0.277 0.301 0.818 0.175] # embeddings of zero [ 0.787 0.355 0.36 0.394 0.236]] # embeddings of word 5
つまり、この操作でサンプル文書内の単語IDに対応する単語の分散ベクトルを取得している。
そして、reshape()で
seq = 3 samples = 2 print emd[target.flatten()].reshape(seq, samples, dims) [[[ 0.299 0.013 0.06 0.801 0.756] # word1 of document1 [ 0.388 0.573 0.055 0.282 0.281]] # word1 of document2 [[ 0.328 0.244 0.967 0.883 0.117] # word2 of document1 [ 0.839 0.759 0.661 0.643 0.883]] # word2 of document2 [[ 0.371 0.033 0.31 0.141 0.847] # word3 of document1 [ 0.895 0.725 0.464 0.907 0.159]]] # word3 of document2
としている。
これでemdの構造が分かった。
次に、
LSTM_W:行列(128×512)
これはこんなイメージ
dims = 5 rand = np.random.rand(dims, dims) w = np.concatenate([rand, rand, rand, rand], axis=1) print w [[ 0.071 0.342 0.38 0.843 0.672 0.071 0.342 0.38 0.843 0.672 0.071 0.342 0.38 0.843 0.672 0.071 0.342 0.38 0.843 0.672] [ 0.717 0.161 0.686 0.376 0.852 0.717 0.161 0.686 0.376 0.852 0.717 0.161 0.686 0.376 0.852 0.717 0.161 0.686 0.376 0.852] [ 0.514 0.514 0.087 0.115 0.008 0.514 0.514 0.087 0.115 0.008 0.514 0.514 0.087 0.115 0.008 0.514 0.514 0.087 0.115 0.008] [ 0.883 0.164 0.708 0.263 0.032 0.883 0.164 0.708 0.263 0.032 0.883 0.164 0.708 0.263 0.032 0.883 0.164 0.708 0.263 0.032] [ 0.135 0.889 0.705 0.503 0.936 0.135 0.889 0.705 0.503 0.936 0.135 0.889 0.705 0.503 0.936 0.135 0.889 0.705 0.503 0.936]]
この2つの内積を取るので、
np.dot(emd, w) [ [ # seq1 # sample1 [ 1.089 1.534 1.24 1.083 1.175 1.089 1.534 1.24 1.083 1.175 1.089 1.534 1.24 1.083 1.175 1.089 1.534 1.24 1.083 1.175] # sample2 [ 0.726 1.217 1.058 0.99 1.321 0.726 1.217 1.058 0.99 1.321 0.726 1.217 1.058 0.99 1.321 0.726 1.217 1.058 0.99 1.321]] [ # seq2 # sample1 [ 1.201 1.092 1.032 1.072 0.789 1.201 1.092 1.032 1.072 0.789 1.201 1.092 1.032 1.072 0.789 1.201 1.092 1.032 1.072 0.789] # sample2 [ 0.729 0.812 1.113 1.219 1.113 0.729 0.812 1.113 1.219 1.113 0.729 0.812 1.113 1.219 1.113 0.729 0.812 1.113 1.219 1.113]] [ # seq3 # sample1 [ 1.779 1.147 1.5 1.032 1.294 1.779 1.147 1.5 1.032 1.294 1.779 1.147 1.5 1.032 1.294 1.779 1.147 1.5 1.032 1.294] # sample2 [ 0.668 0.836 0.664 0.461 0.682 0.668 0.836 0.664 0.461 0.682 0.668 0.836 0.664 0.461 0.682 0.668 0.836 0.664 0.461 0.682]]]
となる。
ポイントは、1単語が512次元ベクトル(上の場合、20次元)から成り、128次元毎に同じ値を繰り返していること。
※3階テンソルと行列の計算は下記にまとめた。
kento1109.hatenablog.com
内積は、(文書の長さ×文書サンプル数×128),(128×512)なので、内積を取った後は、
「文書の長さ×文書サンプル数×512」となる。
このテンソルでstate_belowを更新する。
このテンソルを立方体で書くとこんな感じ。

この内積計算(とバイアスの加算)は、下記の計算と同義と考えられる。
これが、LSTMユニットに渡すための入力となる。
そして、LSTMの核となる部分
rval, updates = theano.scan(_step,
sequences=[mask, state_below],
outputs_info=[tensor.alloc(numpy_floatX(0.),
n_samples,
dim_proj),
tensor.alloc(numpy_floatX(0.),
n_samples,
dim_proj)],
name=_p(prefix, '_layers'),
n_steps=nsteps)
このscanとその関数_stepの理解が一番大事なところ。
まず、構成要素をまとめる。
fn(繰り返し呼び出す関数):
直前で定義された_step関数
sequences(fnに連続的に渡されるオブジェクト):
[mask, state_below]
※maskは、文書の長さ×サンプル数の行列
(文字がある箇所は1、paddingした部分は0となっている)
outputs_info:繰り返し処理の初期値となる値
allocは、指定した値で行列を作る関数
なので、ここではサンプル数×128のゼロ行列を作っている
n_steps(繰り返し回数):
文書の長さ
次にの_stepの内容を見ていく。
def _step(m_, x_, h_, c_): preact = tensor.dot(h_, tparams[_p(prefix, 'U')]) preact += x_ i = tensor.nnet.sigmoid(_slice(preact, 0, options['dim_proj'])) f = tensor.nnet.sigmoid(_slice(preact, 1, options['dim_proj'])) o = tensor.nnet.sigmoid(_slice(preact, 2, options['dim_proj'])) c = tensor.tanh(_slice(preact, 3, options['dim_proj'])) c = f * c_ + i * c c = m_[:, None] * c + (1. - m_)[:, None] * c_ h = o * tensor.tanh(c) h = m_[:, None] * h + (1. - m_)[:, None] * h_ return h, c
まず、引数の整理
m_:maskx_:state_belowh_:サンプル数×128の零行列c_:サンプル数×128の零行列
次に、
preact = tensor.dot(h_, tparams[_p(prefix, 'U')])
preact += x_
LSTMのパラメータにおいて、Uは前の隠れ層の状態からのパラメータを指すのが一般的。
絵にするとこんな感じ。
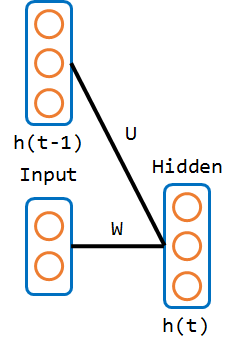
preactは、パラメータUとh_tとの内積
h_tは、「サンプル数×128の行列」、パラメータUは、「128×512の行列」なので、内積を取ると、preactは、「サンプル数×512の行列」となることが分かる。
※初期値は、h_tはゼロ行列なので、preactもゼロ行列となる。
その値にx_tを加算している。
preactは下記の各値を保持していることになる。
※preactは、「pre activation」(活性化前の値」の変数の集まり
LSTMの場合、これがユニットへの入力となる。
絵で示すと赤丸の部分である。

この絵は
Understanding LSTM Networks -- colah's blog
で使用されているもの
パラメータを一つずつ見ていく
まずは、入力ゲート
i = tensor.nnet.sigmoid(_slice(preact, 0, options['dim_proj']))
第二引数に0を指定して_slice関数を呼んでいるので、
def _slice(_x, n, dim): if _x.ndim == 3: # default x.ndim == 2 return _x[:, :, n * dim:(n + 1) * dim] return _x[:, n * dim:(n + 1) * dim] # _x[:,0:128]
のようになる。
これを非線形関数のシグモイド関数で写像する。
つまり、
絵にすると、赤丸の部分。

次に、忘却ゲート(x_tの列が異なるだけ)
f = tensor.nnet.sigmoid(_slice(preact, 1, options['dim_proj']))
つまり、
絵にすると、この部分。
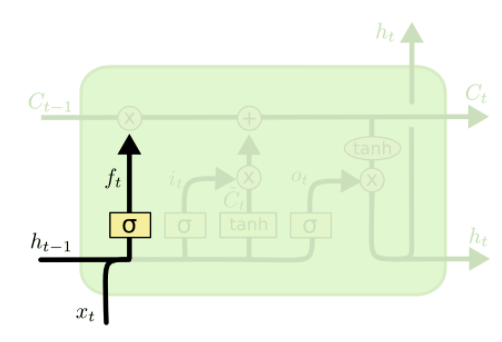
出力ゲートもほとんど同じ。(x_tの列が異なるだけ)
o = tensor.nnet.sigmoid(_slice(preact, 2, options['dim_proj']))
絵にすると、赤丸の部分。

最後に、メモリセル
c = tensor.tanh(_slice(preact, 3, options['dim_proj']))
活性化関数が、tanhだが後はほとんど同じ。
絵にすると、赤丸の部分。

このように、入力に対して、各重みとの線形和をとって非線形関数で写像する。
次に、メモリセルの更新
c = f * c_ + i * c c = m_[:, None] * c + (1. - m_)[:, None] * c_
数式で書くと下記の通り。
絵で表すとこれ。

下の行でmaskとの積で更新している。
maskは、seqのうち、paddingされた箇所に対応する箇所が0となっている。
つまり、単語IDではない部分のcはゼロ更新している。
右側のmaskを反転させたものとc_は、何をしているか分からない・・
とりあえず、先に進める。
最後はLSTMユニットの出力値
h = o * tensor.tanh(c) h = m_[:, None] * h + (1. - m_)[:, None] * h_
数式で書くと下記の通り。
ここでも同様にseqに単語IDがない場合はゼロ更新している。
絵で表すとこれ。
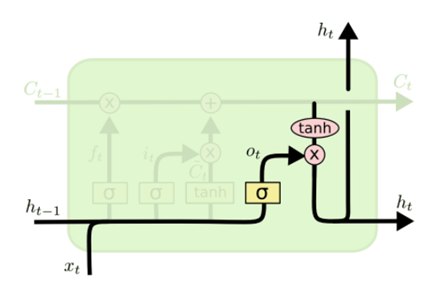
_step関数は、更新したc(メモリセル)とh隠れ層の出力を次のseqの更新で繰り返し利用している。
lstm_layer関数は、最後にreturn rval[0]している。
これで、_step関数の一つ目の戻り値(h)を呼び出し元に返す。
※hは、文字の長さ×サンプル数×隠れ層(128)の3階テンソル。
lstm_layerだけで長くなってしまったので、いったん区切る。