2018-10-08

Pretrained language modelsを理解する

論文 Transfer Learning Language Model

はじめに

少し前に「A Review of the Neural History of Natural Language Processing」というまとめ記事を見ました。
blog.aylien.com

自然言語処理の発展の歴史みたいなもので、近年のブレイクスルーをまとめてくれています。

2018年の注目はELMoに代表される「Pretrained language models」の発展であり、これによりSOTAを達成したとの論文が挙がっています。

ELMoはこちらで分かりやすく解説されています。
kamujun.hatenablog.com

ここでは、自分なりに「Pretrained language models」をまとめようと思います。

Language Model（言語モデル）

言語モデルは文章（単語の並び）に関する確率分布を評価するものです。
ある単語の並びが自然であればその文章の確率は高くなり、不自然であれば低くなります。
言語モデルが学習するのは「自然な単語の並び」です。

数式を使って言語モデルを書いてみます。ここでは、 $w_1,...,w_n$ という $n$ 個の単語からなる文章について考えます。このとき、 $w_1,...,w_n$ という並びで単語が出現する確率は同時確率 $P(w_1,...,w_n)$ で表されます。これは条件付き確率で書くと、
$\begin{eqnarray} P(w_1,...,w_n)=\prod_{t=1}^nP(w_t|w_1,...,w_{t-1}) \end{eqnarray}$
となります。
これは後述する言語モデルと区別するため、「forward LM」（前向き言語モデル）と呼ばれることが多いです。

最近の言語モデルでは、前向き・後ろ向きの両方の言語モデルを利用することが一般的です。
後ろ向き言語モデルは「backward LM」と呼ばれ、下記のような式で表されます。
$\begin{eqnarray} P(w_1,...,w_n)=\prod_{t=1}^nP(w_t|w_{t+1},...,w_n) \end{eqnarray}$

イメージとしてはこんな感じです。
f:id:kento1109:20181008110529p:plain

2つ合わせて「biLMs」（双方向言語モデル）と呼びます。

「are」という単語の出現確率の計算に「前の単語の並び」だけではなく、「後ろの単語の並び」も利用します。

双方向の並びを学習することで、中間層の重みが言語モデルを最適化するように調整されます。
最終的にはその重みを結合させます。

f:id:kento1109:20181025164901p:plain

※上の２つはThe Bidirectional Language Model – Motoki Wu – Mediumより引用

「word2vec」などの事前学習で獲得した分散表現を入力層の初期パラメータとすることで自然言語処理のタスクの精度が向上することが知られています。
ただし、入力層に渡される文章の分散表現は単語を順番に並べただけであり、当然ですが文脈情報は含まれていません。
一方、双方向の言語モデルで学習された分散表現の場合、文脈情報が考慮されております。

このあたりが「文脈情報を考慮した分散表現」としてSOTAに貢献しているのかなとも思いました。

ELMo

ELMoで学習した単語の分散表現は以下のように目的のタスクに結合させます。
f:id:kento1109:20181025174941p:plain

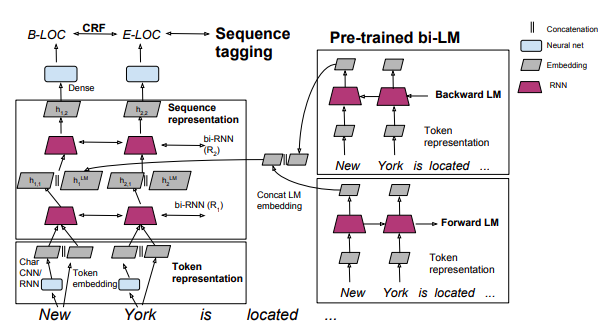
※http://ai2-website.s3.amazonaws.com/publications/semi-supervised-sequence.pdfより引用

通常の単語の分散表現は、文章中の単語を分散表現に変換したものの集まりです。
一方、biLMsの分散表現は、文章を言語モデルに通して得られたものです。
上記の例だと、単語「York」の分散表現は、forward LMを通して、「New」の単語ベクトルの情報も含んでいます。また、backward LMを通して、「is located ...」の単語ベクトルの情報も含んでいます。

ELMoの応用

まず、タスクの対象言語が日本語の場合は日本語の言語モデルを使う必要があります。そのため、ELMoなどの既存の学習済のモデルをそのまま使うことは出来ません。
また、タスクがドメイン依存する場合、Wikipedia等のコーパスで学習した言語モデルがどの程度有効かは分かりません。
次回はドメインに依存するタスクでの言語モデルについてまとめたいと思います。

参考

以下の解説ページが分かりやすかったです。

2018-10-03

Pytorch：テキストの前処理（torchtext）③

PyTorch torchtext メモ

はじめに

torchtextの使い方メモ第三弾。

前回の内容は下記参照
kento1109.hatenablog.com

今回の内容は１つだけ。
POSやNERなどのTaggingを考える場合、どのようにtorchtextで読み込めばよいか。

前回まではtorchtextでデータをファイルから読む際、想定されているのは（感情分析等の場合）以下のような形式だった。

I love this moive,1

ただし、学習の目的がTaggingの場合、入力データのフォーマットがそもそも異なる。
NERの場合、だいたいこんな感じだ。

Tom B-PER
is O
my O
friend O

New B-LOC
York I-LOC
is O
always O
crowded O

行ごとに単語が並んでおり、それぞれにタグが付与されている。
文章の区切りは、CoNLLのデータセットの場合、空行で行われる。

こんなフォーマットの場合、どのように処理すればよいだろう。
結論から言うと、SequenceTaggingDatasetを使う。以上だ。

SequenceTaggingDataset

先ほどのデータの場合、以下のようにして読み込む。

from torchtext import data, datasets

TEXT = data.Field()
LABEL = data.Field()

train = datasets.SequenceTaggingDataset(
        path='test.tsv',
        fields=[('text', TEXT), ('label', LABEL)])

すると、以下のようにセンテンス単位となる。

print(vars(train[0]))
# {'text': ['Tom', 'is', 'my', 'friend'], 'label': ['B-PER', 'O', 'O', 'O']}

必要に応じて

TEXT = data.Field(init_token='<bos>', eos_token='<eos>')
LABEL = data.Field(init_token='<bos>', eos_token='<eos>')

とすると、文の先頭と末尾に記号をつけることが出来る。

センテンスの単位であるが、github.com
にあるSequenceTaggingDatasetクラスをみれば分かるが、行が空白の場合、それまでの単語・ラベルをセンテンスとしてまとめる処理をしている。（31行目あたり）

datasetsさえ作れれば、後の処理は前回と同じ。
前回と同じ書き方で辞書も作れる。

TEXT.build_vocab(train)
vocab = TEXT.vocab
vocab.itos
['<unk>',
 '<pad>',
 'is',
 'New',
 'Tom',
 'York',
 'always',
 'crowded',
 'friend',
 'my']

大した内容ではないが、少し嵌ったのでメモした。

2018-09-30

Neo4jを触ってみる

Neo4j

はじめに

自然言語処理を勉強していると、オントロジーやシソーラスってのが出てくる。
オントロジーやシソーラスを勉強すると、グラフ理論ってのが出てくる。
グラフ理論を勉強すると、グラフDBとして有名な「Neo4j」が出てくる。

ということで、今回はNeo4jの基本的なことを勉強したのでまとめようと思う。

以下の内容は公式サイトのドキュメントより引用したものが、ほとんどなので詳しく知りたい場合はそっちを見るのが良い。
neo4j.com

Property Graph Model

Neo4jは、Property Graph Modelと呼ばれている。これは、各ノードがプロパティを持ち、ノード情報を格納するモデル。
グラフ構造の基本形はこんな感じ。
f:id:kento1109:20180930115848p:plain

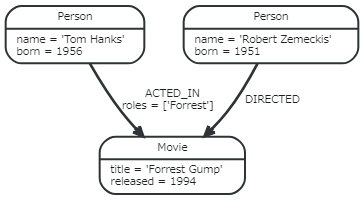
各構成要素を簡単に説明をする。

ノード

しばしば「エンティティ」を表現される。
1つの実体を表す構成単位みたいなもの。
f:id:kento1109:20180930120002p:plain

プロパティ付きで単一をノードを作成するには、

CREATE (n {name: {key1:value1, key2:value2, ...}})

と書く。

関係

ノード間をつなぐ要素。関係を定義してこそのグラフDB。
f:id:kento1109:20180930120525p:plain
Neo4jは有向グラフなので、ノードの向きも合わせて定義する必要がある。

ノード間の関係を定義するには、

CREATE （identifier）-[:name]->（identifier）

と書く。

プロパティ（属性）

ノードや関係などが持つ実際の値。
ノードの例だと、nameやbornが各プロパティ。関係の場合、rolesがプロパティ。

ラベル

グラフ構造体と呼ばれる複数のノードを１つにまとめるために使われる。オントロジーで言うところの「概念」みたいなもので、世界（ノード）をラベルを付けて、概念化する。
ノードの図で言うと、上のノードには「Person」ラベルがついており、下のラベルには「Movie」ラベルがついていることが分かる。オントロジー上ではPersonやMovieはあくまで概念に過ぎないが、それをインスタンス化してあげると、各エンティティ（ノード）が出来あがるようなイメージ。

ノード・ラベル・プロパティの関係を図示するとこんな感じ。
f:id:kento1109:20180930121915p:plain:w160
（Cypher Query Language(QL)-初級編 #neo4j - クリエーションライン株式会社
より引用）

識別子

ノードや関係性、処理結果などの値を示す構造体。
上の構成要素と異なり、処理中に用いるものに過ぎないが、知っておかないとラベルとの違いに少し混乱する。
こんな感じでノードを表してみる。（emilが識別子）

emil:Person {name:'Emil'}

そうすると、emilがPerson {name:'Emil'}というノード情報を保持した構造体として記憶される。

一般的な使用方法としては、ノードと関係を作成するような例。

CREATE (TheMatrix:Movie {title:'The Matrix', released:1999})
CREATE (Keanu:Person {name:'Keanu Reeves', born:1964})
CREATE (Keanu)-[:ACTED_IN {roles:['Neo']}]->(TheMatrix)

作成されたノードに識別子の情報は一切持たないので、そのノードを使って後の文で処理しないのであれば、名前にこだわる必要は全くない。

どういうことかと言うと、

CREATE (TheMatrix:Movie {title:'The Matrix', released:1999})
CREATE (Keanu:Person {name:'Keanu Reeves', born:1964})

を宣言した後で別のクエリで

CREATE (Keanu)-[:ACTED_IN {roles:['Neo']}]->(TheMatrix)

としても上の識別子のノードではなく、新しいノードが作られてしまう。

最低限こんなこととクエリの書き方さえ覚えればOKかと思う。

2018-09-29

Stan：NMF

はじめに

今回はNMF(Non-negative Matrix Factorization）について勉強する。
日本語では「非負値行列因子分解」と言い、線形次元手法の１つ。
その名前の通り「観測データの非負性」を仮定したモデル。
「非負性」の制約を設けることで、これに適用可能な観測データはより良い表現ができるらしい。
推薦アルゴリズムなどでも使われている。

詳しいことは省略して実装するうえで大事なところを押さえていく。MCMCではなく、最適化により求める方法は「非負値行列因子分解 - NTTコミュニケーション科学基礎研究所」がとても丁寧だった。

尚、今回の記事のいくつかは「ベイズ推論による機械学習入門」を参考とした。

NMF

まず、観測データ（各要素が非負値の行列）行列 $\rm{X}\in \mathbb{R}^{D\times N}$ を以下のように表す。
$\rm{X}\approx\rm{WH}$
尚、 $\rm{W}\in \mathbb{R}^{D\times M}$ ・ $\rm{H}\in \mathbb{M}^{M\times N}$
$M$ は観測データに出現しない潜在変数である。
$\rm{X}$ を要素ごとに書くと次のようになる。
$X_{d,n}\approx\sum_{m=1}^M W_{d,m}H_{m,n}$
例えば、行列 $\rm{X}$ がユーザー×アイテムのレーティング値の場合、 $\rm{W}$ はユーザー×潜在変数（ユーザーの嗜好）を表し、行列 $\rm{H}$ は潜在変数×アイテム（アイテムの特徴）のようなものを表している。
この場合、ユーザー $d$ のアイテム $n$ への評価は、ユーザー $d$ の嗜好ベクトルとアイテム $n$ の特徴ベクトルの内積で決定される。２つのベクトルの方向が近い（ユーザー $d$ の嗜好とアイテム $n$ の特徴が近い）ほど、レーティング値は大きくなるようになる。

モデル

今回は観測データの要素が非負の整数を仮定したモデルを考える。
非負の整数なので、データ生成にはポアソン分布が使える。
各要素は以下のように表せたので、
$X_{d,n}\approx\sum_{m=1}^M W_{d,m}H_{m,n}$
これをそのままポアソン分布にあてはめる。
$p(X_{d,n})\sim{\rm Poi} (X_{d,n}|\sum_{m=1}^M W_{d,m}H_{m,n})$

今回はこれが尤度となる。（計算では対数を取る。）
NMFで目指すのは、 $\rm{X}$ を $\rm{WH}$ で近似させること。
各要素 $X_{d,n}$ と $sum_{m=1}^M W_{d,m}H_{m,n}$ が近似できているかどうかは「尤度」で測ることができる。
ポアソン分布の場合、観測値が平均値と一致する値が尤度最大となる値である。この場合、 $X_{d,n}=sum_{m=1}^M W_{d,m}H_{m,n}$ である。観測値が平均から離れるほど尤度は小さくなる
簡単であるが、ポアソン分布での尤度を比べてみた。

dpois(1,1,log=TRUE)
[1] -1
dpois(1,5,log=TRUE)
[1] -3.390562

観測値と平均値が近いほど、尤度が大きいことが分かる。
NMFではポアソン分布の尤度を大きくすることが、 $\rm{X}$ を $\rm{WH}$ させることと同じ意味なのである。

行列全体の尤度は以下のように各要素の積で書ける。
$\begin{eqnarray} L &=& \prod_{d=1}^D\prod_{n=1}^N {\rm Poi} (X_{d,n}|\sum_{m=1}^M W_{d,m}H_{m,n}) \\ \log L &=& \sum_{d=1}^D\sum_{n=1}^N \log{\rm Poi} (X_{d,n}|\sum_{m=1}^M W_{d,m}H_{m,n}) \end{eqnarray}$

$W,H$ の各要素は、ガンマ分布を取っておくのが良いと思われる。
$p(W_{d,m})\sim{\rm Gam}(W_{d,m}|a,b)$
$p(H_{m,n})\sim{\rm Gam}(H_{d,m}|a,b)$

コード

コードは以下の通り。
（以前、ネットに落ちていたのを少し改良した。）

data{
  int<lower=1> D; // row dimension of input
  int<lower=1> N; // column dimension of input
  int<lower=1> M; // hidden dimension
  
  int X[D,N]; // original data
  
  real<lower=0> alpha; //hyperparameter
  real<lower=0> beta; //hyperparameter
}

parameters{
  matrix<lower=0>[D, M] W;
  matrix<lower=0>[M, N] H;
}


model{
  //estimate W matrix dist
  for(d in 1:D){
    for(m in 1:M){
      W[d,m] ~ gamma(alpha,beta);
    }
  }
  //estimate H matrix dist
  for(m in 1:M){
    for(n in 1:N){
      H[m,n] ~ gamma(alpha,beta);
    }
  }

  for(d in 1:D){
      for(n in 1:N){
        target += poisson_lpmf(X[d,n] | sum(W[d,:])*sum(H[:,n]));
      }
  }
}

以下のようにしてキックする。

stan.dat <- list(D=nrow(data),D=ncol(data),M=2,X=data,alpha=0.1,beta=0.1)
stan.fit <- stan("NMF.stan", data=stan.dat)

ちなみにデータはこんな感じ。

data
  item1 item2 item3 item4 item5 item6 item7 item8 item9 item10
1     0     2     4     1     0     0     0     1     2      5
2     0     2     3     0     0     0     1     2     2      3
3     1     0     1     4     3     0     1     1     1      0
4     0     0     1     4     5     1     0     1     2      1
5     1     1     5     4     1     1     1     0     1      5

収束はするがデータが小さいので面白い発見は出来ない・・

今回は観測データが非負の整数を取ったが、取る範囲が広いほど推論が難しい気がする。観測データが二値でベルヌーイ分布でやってみるのも面白いかもしれない。

2018-08-13

Pytorch：ライブラリの誤差関数の構造を理解する

PyTorch

はじめに

今まで当たり前のように誤差関数を使っていた。
既に用意されたものであればそれで問題ない。

しかし、誤差関数を自作したいと思った場合、
ライブラリの誤差関数の構造を理解している必要がある。

そんなわけでライブラリの誤差関数について調べたのでメモ。

簡単な復習

簡単に使い方を復習する。

ライブラリの誤差関数を利用する場合、以下のような使い方をする。

import torch
import torch.nn as nn
import torch.nn.functional as F

net = Net() 
outputs = net(inputs)

criterion = nn.MSELoss()

loss = criterion(outputs, targets)
loss.backward()

ネットワーク

今回はシンプルな以下のネットワークを考える。

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(32, 16)
        self.fc2 = nn.Linear(16, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

パラメータは以下の通り

params = list(net.parameters())
print(params[0].size())
torch.Size([16, 32])

print(params[1].size())
torch.Size([16])

print(params[1])
Parameter containing:
tensor([ 0.0982,  0.0495,  0.1656, -0.1646,  0.1014, -0.0163, -0.0873,
         0.0418, -0.0404,  0.1556, -0.1247,  0.0236, -0.0651,  0.0960,
         0.1342,  0.1203])

入力

以下のように入力データを作成する。

torch.manual_seed(1)

inputs = torch.randn(10, 32)
targets = torch.randn(10)
targets = targets.view(1, -1)
print(targets)
tensor([[ 0.1924,  0.7161, -0.8120, -1.4617,  0.2328,  0.1896, -0.2204,
          0.1491,  0.0100, -0.1243]])

出力

出力結果は以下の通り

outputs = net(inputs)
outputs = outputs.view(1, -1)
print(outputs)
tensor([[-0.2504,  0.0378,  0.1485,  0.1909, -0.1019,  0.2417,  0.1653,
          0.1359, -0.1187,  0.0876]])

誤差計算

まず、誤差関数のインスタンスを生成する。

criterion = nn.MSELoss()

次に出力結果と真の値を誤差関数の入力として、誤差を求める。

outputs = outputs.view(1, -1)
loss = criterion(outputs, targets)
print(loss)
tensor(0.4635)

Backprop

求めた誤差からパラメータの勾配を計算する。

net.zero_grad()

print(net.fc2.weight.grad)
> None
loss.backward()
print(net.fc2.weight.grad)
tensor([[ 0.0611,  0.0976, -0.2338,  0.1976,  0.0020, -0.0788, -0.1145,
         -0.1976,  0.0699, -0.3314,  0.2379, -0.0534,  0.0729, -0.0008,
         -0.2456, -0.2657]])

はじめは勾配がNoneとなっているが、loss.backward()により、勾配ベクトルが計算されていることが分かる。

パラメータ更新（最適化）
今回は確率的勾配降下法（SGD）を用いた。

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

sub_でその値から引数の値を引き算する。

更新後の誤差を確認する。

outputs = net(inputs)
outputs = outputs.view(1, -1)

loss = criterion(outputs, targets)
print(loss)
tensor(0.3956)

誤差が減少していることが確認できた。

実際は多くの最適化関数も用意されているのでそちらを利用する方が良い。

import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.01)
optimizer.step()

参考：
Neural Networks — PyTorch Tutorials 0.4.1 documentation

基本的なことを復習したところで、もう少し深く理解する。

nn.MSELoss()

ソースを覗いてみる。
torch.nn.modules.loss — PyTorch master documentation

class MSELoss(_Loss):
    def __init__(self, size_average=None, reduce=None, reduction='elementwise_mean'):
        super(MSELoss, self).__init__(size_average, reduce, reduction)

    def forward(self, input, target):
        return F.mse_loss(input, target, reduction=self.reduction)

※長かったのでコメントは省略
実装部分は意外とシンプルでコンストラクタとforward関数のみのクラス。
他の誤差関数も同じようなクラス構造。

F.mse_loss自体が実際に平均二乗誤差を計算している関数。

このクラスが継承している_Lossとは何か。

class _Loss(Module):
    def __init__(self, size_average=None, reduce=None, reduction='elementwise_mean'):
        super(_Loss, self).__init__()
        if size_average is not None or reduce is not None:
            self.reduction = _Reduction.legacy_get_string(size_average, reduce)
        else:
            self.reduction = reduction

このクラス自体はModuleを継承している。

てな感じでみていくと誤差関数のクラスは以下の構造でOKと思われる。

class LossFunction(nn.Module):

def __init__(self):
    super(LossFunction, self).__init__()

def forward(self, inputs, targets):
   loss = function(inputs, targets)
   return loss

ただし、必ずクラス構造である必要はなく、誤差関数だけでも良い。
実際に以下でも正しくパラメータ更新ができた。

loss = F.mse_loss(outputs, targets)

2018-08-12

Stan：TwoCountryQuiz②

Stan

はじめに

前回は「コワイ本」のTwoCountryQuizのタスクに取り組んだ。

今回はこの続きについてまとめる。

ラベルスイッチング

前回のモデルは事後分布が二峰性をもつような分布となっていた。
この原因として「ラベルスイッチング」が原因だと述べた。
混合モデルを考える場合、これはやはり避けて通れない。

はじめに「何故そう考えたか」について尤度計算を交えて説明する。
まず、今回のデータ（TwoCountryQuiz）は以下のような行列だった。

	A	B	...	H
人1	1	0	...	1
人2	1	0	...	1
...	...	...	...	...
人8	0	1	...	0

そして、

人1が「タイ人かどうか」
問題Aが「タイの歴史に関するものかどうか」

を推論することが今回の目的だった。

これは以下の推論でも構わない。

人1が「モルドバ人かどうか」
問題Aが「モルドバの歴史に関するものかどうか」

そして、当たり前だがモデルはユーザーがどっちを想定しているかなど知らない。

この推論が同じ結果になることを尤度計算により確認する。

全体尤度の計算は以下の通り。
$\begin{eqnarray} L &=& \prod_{i=1}^{nx}\prod_{j=1}^{zj}\left( \begin{array}{ccc} (1-p(x_i))\times(1-p(z_j)) \times {\rm Bern}(k_{i,j}|\alpha)\\ + \\ p(x_i)\times p(z_j) \times {\rm Bern}(k_{i,j}|\alpha)\\ + \\ (1-p(x_i))\times p(z_j) \times {\rm Bern}(k_{i,j}|\beta)\\ + \\ p(x_i)\times (1-p(z_j)) \times {\rm Bern}(k_{i,j}|\beta)\\ \end{array} \right) \end{eqnarray}$

対数を取ると以下の通り。

$\begin{eqnarray} \log L &=& \sum_{i=1}^{nx}\sum_{j=1}^{zj} \log\left( \begin{array}{ccc} (1-p(x_i))\times (1-p(z_j)) \times {\rm Bern}(k_{i,j}|\alpha)\\ + \\ p(x_i)\times p(z_j) \times {\rm Bern}(k_{i,j}|\alpha)\\ + \\ (1-p(x_i))\times p(z_j) \times {\rm Bern}(k_{i,j}|\beta)\\ + \\ p(x_i)\times (1-p(z_j)) \times {\rm Bern}(k_{i,j}|\beta)\\ \end{array} \right) \end{eqnarray}$

log_sum_expを使うと以下の通り。

$\begin{eqnarray} \log L &=& \sum_{i=1}^{nx}\sum_{j=1}^{zj} {\rm log\_sum\_exp}\left( \begin{array}{ccc} \log(1-p(x_i))+\log(1-p(z_j)) + \log{\rm Bern}(k_{i,j}|\alpha)\\ \log p(x_i)+\log p(z_j) +\log {\rm Bern}(k_{i,j}|\alpha)\\ \log(1-p(x_i))+\log p(z_j) +\log{\rm Bern}(k_{i,j}|\beta)\\ \log p(x_i)+ \log(1-p(z_j)) +\log {\rm Bern}(k_{i,j}|\beta)\\ \end{array} \right) \end{eqnarray}$

※各式の意味に関しては前回参照

実際に人1の問題Aに関する尤度を計算する。
尚、計算時点でのパラメータは以下で与えられたとする。

$\alpha=0.8$
$\beta=0.1$
$x_1=0.2$
$z_1=0.3$

計算結果は以下の通り。

$\begin{eqnarray} \log L_{1,1} &=& {\rm log\_sum\_exp}\left( \begin{array}{ccc} \log (0.8)+\log (0.7) + \log{\rm Bern}(1|0.8)\\ \log (0.2)+\log (0.3) + \log{\rm Bern}(1|0.8)\\ \log (0.8)+\log (0.3) + \log{\rm Bern}(1|0.1)\\ \log (0.2)+\log (0.7) + \log{\rm Bern}(1|0.1)\\ \end{array} \right)\\ &=& {\rm log\_sum\_exp}\left( \begin{array}{ccc}-0.8\\-3.03\\-3.72\\-4.27 \end{array} \right)\\ &=&-0.62 \end{eqnarray}$

他のパラメータを固定したもとで $z_1=0.7$ に更新すると尤度はどう変化するか確認する。
計算結果は以下の通り。

$\begin{eqnarray} \log L_{1,1} &=& {\rm log\_sum\_exp}\left( \begin{array}{ccc} \log (0.8)+\log (0.3) + \log{\rm Bern}(1|0.8)\\ \log (0.2)+\log (0.7) + \log{\rm Bern}(1|0.8)\\ \log (0.8)+\log (0.7) + \log{\rm Bern}(1|0.1)\\ \log (0.2)+\log (0.3) + \log{\rm Bern}(1|0.1)\\ \end{array} \right)\\ &=&{\rm log\_sum\_exp}\left( \begin{array}{ccc}-1.64\\-2.19\\-2.88\\-5.11 \end{array} \right)\\ &=&-0.99 \end{eqnarray}$

尤度が小さくなることが分かる。
これは、「各人がタイ人（モルドバ人）であるとき、問題がモルドバ（タイ）の歴史」としたの場合の尤度に近い（確率なので同じではない）ので尤度が小さくなる。

では、この条件下で $x_1=0.8$ に更新すると尤度はどう変化するか。

$\begin{eqnarray} \log L_{1,1} &=& {\rm log\_sum\_exp}\left( \begin{array}{ccc} \log (0.2)+\log (0.3) + \log{\rm Bern}(1|0.8)\\ \log (0.8)+\log (0.7) + \log{\rm Bern}(1|0.8)\\ \log (0.2)+\log (0.7) + \log{\rm Bern}(1|0.1)\\ \log (0.8)+\log (0.3) + \log{\rm Bern}(1|0.1)\\ \end{array} \right)\\ &=& {\rm log\_sum\_exp}\left( \begin{array}{ccc}-0.8\\-3.03\\-4.27\\-3.72 \end{array} \right)\\ &=&-0.62 \end{eqnarray}$

最初のパラメータでの尤度と等しくなる。
つまり、 $\alpha,\beta$ に関係なく、 $x_1=0.2,z_1=0.3$ と $x_1=0.8,z_1=0.7$ での尤度は等しくなるというわけである。
そんな訳で尤度を大きくするパラメータは、 $x_1=0.2$ でも $x_1=0.8$ でも[z_1]によっては尤度が同じということになり、事後分布が二峰性を持つことになるのである。

パラメータの制約

では、どうすればよいか。
問題は $x_1=0.2$ でも $x_1=0.8$ 尤度が同じになるということだった。では、 $x_1$ が取れる範囲を制約してしまおうというのが１つの対処法である。
例えば、 $x_1>0.5$ の制約を設けることで、その制約下で尤度を大きくするための $z_1$ を探索する。
実装方法としては以下のような書き方が考えられる。

parameters {
  real<lower=0.5, upper=1> init_x_prob;
  real<lower=0, upper=1> other_x_prob[nx-1];
}
transformed parameters {
  real x_prob[nx];
  x_prob[1] = init_x_prob;
  for(i in 1:nx-1)
    x_prob[i+1] = other_x_prob[i];
}

これで $x_1$ の乱数生成を $0.5\sim1.0$ に制限する。
※ベクトルの１要素のみに制約を設定する方法は既にグーグルフォーラムで挙がっていたので参考とさせて頂いた。
Google グループ

モデリング

全体のStanは以下の通り。
$x_1$ の制約以外はほとんど前と同じ。

data{
  int<lower=1> nx;              // num person
  int<lower=1> nz;              // num question
  int<lower=0, upper=1> k[nx, nz];   // person * question
}
parameters {
  real<lower=0.5, upper=1> init_x_prob;
  real<lower=0, upper=1> other_x_prob[nx-1];
  real<lower=0, upper=1> z_prob[nz];
  real<lower=0, upper=1> alpha;
  real<lower=0, upper=alpha> beta;
}
transformed parameters {
  real x_prob[nx];
  x_prob[1] = init_x_prob;
  for(i in 1:nx-1)
    x_prob[i+1] = other_x_prob[i];
}
model {
  vector[4] lp;
  //for(i in 1:nx)
  //  x_prob[i] ~ beta(a,b);;  // prior
  //for(j in 1:nz)
  //  z_prob[j] ~ beta(a,b);;  // prior
  for(i in 1:nx){
    for(j in 1:nz){
      lp[1] = (log1m(x_prob[i]) + log1m(z_prob[j]) + bernoulli_lpmf(k[i, j]| alpha));
      lp[2] = (log(x_prob[i]) + log(z_prob[j]) + bernoulli_lpmf(k[i, j]| alpha));
      lp[3] = (log1m(x_prob[i]) + log(z_prob[j]) + bernoulli_lpmf(k[i, j]| beta));
      lp[4] = (log(x_prob[i]) + log1m(z_prob[j]) + bernoulli_lpmf(k[i, j]| beta));
      target += log_sum_exp(lp);
    }
  }
}

結果の確認

実行結果は以下の通り。

stan.fit <- stan("TwoCountryQuiz.stan",data=stan.dat,pars=c('x_prob','z_prob'))

summary(stan.fit)
$summary
                 mean     se_mean        sd          2.5%          25%         50%
x_prob[1]   0.8257743 0.004583606 0.1372088   0.528647083   0.73226802   0.8620697
x_prob[2]   0.7505101 0.013206512 0.2454967   0.077761085   0.65885906   0.8371625
x_prob[3]   0.2848253 0.011180096 0.2422784   0.008530586   0.09599669   0.2132672
x_prob[4]   0.3344115 0.008289728 0.2467132   0.017356223   0.13546493   0.2774034
x_prob[5]   0.7564982 0.013374523 0.2441466   0.090157994   0.66361202   0.8418284
x_prob[6]   0.7106300 0.011092027 0.2467630   0.087634316   0.57762401   0.7808384
x_prob[7]   0.2776645 0.010963704 0.2489371   0.007548964   0.08553814   0.1958664
x_prob[8]   0.2905203 0.010156586 0.2449326   0.007862108   0.09827746   0.2208900
z_prob[1]   0.7189481 0.010696188 0.2444943   0.085165215   0.60045169   0.7911544
z_prob[2]   0.2712665 0.010862294 0.2398265   0.009096772   0.08682635   0.1975436
z_prob[3]   0.3250752 0.007364386 0.2474678   0.015272428   0.12510105   0.2692455
z_prob[4]   0.7139130 0.011395878 0.2432047   0.099609097   0.59076957   0.7835717
z_prob[5]   0.7556119 0.012485880 0.2441034   0.091712754   0.65056501   0.8450558
z_prob[6]   0.2471072 0.012882019 0.2460234   0.004999654   0.06493085   0.1560054
z_prob[7]   0.2848787 0.012258488 0.2448348   0.010895594   0.09539916   0.2123684
z_prob[8]   0.7588505 0.012929736 0.2370986   0.105125385   0.66719031   0.8418040
lp__      -76.6538982 0.173507422 4.0323283 -85.464497249 -79.14733785 -76.2325885
                  75%       97.5%     n_eff     Rhat
x_prob[1]   0.9405903   0.9950119  896.0852 1.002287
x_prob[2]   0.9309936   0.9919926  345.5532 1.005609
x_prob[3]   0.4083455   0.9058809  469.6110 1.002421
x_prob[4]   0.4877216   0.9151902  885.7355 1.002222
x_prob[5]   0.9374089   0.9953916  333.2304 1.006969
x_prob[6]   0.9068108   0.9915599  494.9237 1.002667
x_prob[7]   0.4008561   0.9103599  515.5425 1.004395
x_prob[8]   0.4202415   0.9004982  581.5642 1.004779
z_prob[1]   0.9100841   0.9919731  522.4915 1.004377
z_prob[2]   0.3818967   0.9177776  487.4739 1.005363
z_prob[3]   0.4726530   0.9227644 1129.1828 1.001313
z_prob[4]   0.9048383   0.9913114  455.4579 1.002746
z_prob[5]   0.9364634   0.9945814  382.2165 1.003059
z_prob[6]   0.3527158   0.9079530  364.7412 1.005107
z_prob[7]   0.4027377   0.9158467  398.9079 1.005976
z_prob[8]   0.9324511   0.9944236  336.2627 1.007949
lp__      -73.6854277 -70.1485710  540.1018 1.002221

収束判定は問題なさそう。
確率も前回のような0.5周辺ではなく、きっちり分かれている。

事後分布

前回、二峰性だった事後分布を確認する。

stan_dens(stan.fit,pars ="x_prob[1]",separate_chains = TRUE)

f:id:kento1109:20180705232218p:plain
単峰性の分布であることが確認できる。chainによるバラツキもあまりない。裾野が長いのが気になるが、これはサンプル数の問題と思われる。（後で検証してみる。）
一応、制約を加えなかったパラメータも確認する。

stan_dens(stan.fit,pars ="x_prob[3]",separate_chains = TRUE)

f:id:kento1109:20180705232758p:plain
二峰性は見られないことが分かる。

トレース結果

stan_trace(stan.fit,pars = "x_prob[1]")

f:id:kento1109:20180705232526p:plain
制約を加えたこともあり、制約範囲内で動いている。（非常に分散が大きいのが少し気にがるが・・）
同様に制約を加えなかったパラメータも確認する。

stan_trace(stan.fit,pars = "x_prob[3]")

f:id:kento1109:20180705232916p:plain
分散は大きいが $0\sim0.3$ あたりで多くサンプリングされていることが分かる。

サンプル数を増やしてモデリング

最後にサンプル数を24人に増やして再度モデリングを行った。
（データセットは単純に8人分のデータ×3しただけ）

結果は以下の通り。

summary(stan.fit)
$summary
                    mean      se_mean         sd          2.5%           25%
x_prob[1]     0.88909723 0.0015264536 0.09654140  6.379189e-01    0.84088896
x_prob[2]     0.88306846 0.0017073929 0.10798501  5.979277e-01    0.83358725
x_prob[3]     0.17779696 0.0022253553 0.14074382  6.284815e-03    0.06514292
x_prob[4]     0.24431969 0.0026401563 0.16697814  1.462065e-02    0.11160276
x_prob[5]     0.88339388 0.0016822210 0.10639300  5.915050e-01    0.83695690
x_prob[6]     0.82474879 0.0021329165 0.13489748  4.874794e-01    0.74488734
x_prob[7]     0.15902617 0.0020105498 0.12715834  5.048530e-03    0.05834003
x_prob[8]     0.17922045 0.0021341862 0.13497779  7.067403e-03    0.07218645
x_prob[9]     0.88388361 0.0016258287 0.10282643  6.155001e-01    0.83528646
x_prob[10]    0.88482958 0.0016178430 0.10232138  6.219439e-01    0.83460776
x_prob[11]    0.17376721 0.0021239378 0.13432962  7.741369e-03    0.07019395
x_prob[12]    0.24658736 0.0025807395 0.16322030  1.360339e-02    0.11582604
x_prob[13]    0.88225775 0.0016771932 0.10607501  6.072548e-01    0.82842426
x_prob[14]    0.82616041 0.0021704359 0.13727042  4.905692e-01    0.74875851
x_prob[15]    0.15963763 0.0021007873 0.13286546  4.750483e-03    0.05315915
x_prob[16]    0.18142896 0.0021570449 0.13642350  6.887512e-03    0.07567072
x_prob[17]    0.88654126 0.0016228331 0.10263698  6.202509e-01    0.83865202
x_prob[18]    0.88467146 0.0016392687 0.10367646  6.029201e-01    0.83315147
x_prob[19]    0.17220191 0.0021321826 0.13485107  6.665817e-03    0.06455919
x_prob[20]    0.24572632 0.0026661863 0.16862443  1.241102e-02    0.11079253
x_prob[21]    0.88259919 0.0016423417 0.10387081  6.201909e-01    0.83208995
x_prob[22]    0.82613928 0.0022048355 0.13944604  4.796073e-01    0.75000947
x_prob[23]    0.15867396 0.0020519952 0.12977957  5.023390e-03    0.05646634
x_prob[24]    0.18281938 0.0021713075 0.13732554  9.281820e-03    0.07586258
z_prob[1]     0.90059791 0.0013291991 0.08406593  6.808949e-01    0.85748083
z_prob[2]     0.08281926 0.0011276441 0.07131847  2.591367e-03    0.02921736
z_prob[3]     0.16589135 0.0018243489 0.11538195  6.090128e-03    0.07509763
z_prob[4]     0.89537937 0.0013233079 0.08369334  6.885263e-01    0.85128247
z_prob[5]     0.94851652 0.0007727115 0.04887056  8.209348e-01    0.92862688
z_prob[6]     0.05198457 0.0007983830 0.05049418  1.322733e-03    0.01514927
z_prob[7]     0.09923228 0.0012919329 0.08170901  3.422783e-03    0.03655729
z_prob[8]     0.94831005 0.0008012587 0.05067605  8.110328e-01    0.92770249
lp__       -165.12638755 0.1230833587 4.69380930 -1.754599e+02 -167.91580233
                     50%          75%        97.5%    n_eff      Rhat
x_prob[1]     0.91570868    0.9632312    0.9965173 4000.000 1.0000139
x_prob[2]     0.91501176    0.9641354    0.9965150 4000.000 0.9997085
x_prob[3]     0.14653449    0.2576420    0.5169342 4000.000 0.9991991
x_prob[4]     0.21428473    0.3508085    0.6205980 4000.000 0.9994822
x_prob[5]     0.91291980    0.9619288    0.9971203 4000.000 0.9994962
x_prob[6]     0.85376265    0.9305850    0.9914166 4000.000 0.9991922
x_prob[7]     0.12972880    0.2282888    0.4739765 4000.000 0.9999588
x_prob[8]     0.15058849    0.2521316    0.5022369 4000.000 0.9998293
x_prob[9]     0.91202499    0.9622890    0.9963306 4000.000 0.9999095
x_prob[10]    0.91357950    0.9628045    0.9967515 4000.000 0.9998023
x_prob[11]    0.14187091    0.2502796    0.4986213 4000.000 0.9994550
x_prob[12]    0.22103501    0.3514679    0.6198173 4000.000 1.0002860
x_prob[13]    0.91473044    0.9630547    0.9967746 4000.000 0.9994394
x_prob[14]    0.85865190    0.9357102    0.9948808 4000.000 0.9998928
x_prob[15]    0.12518733    0.2320583    0.4899430 4000.000 0.9995863
x_prob[16]    0.15374736    0.2578792    0.5127041 4000.000 0.9997273
x_prob[17]    0.91694762    0.9645227    0.9965024 4000.000 0.9995645
x_prob[18]    0.91524153    0.9621940    0.9968299 4000.000 0.9993828
x_prob[19]    0.14001510    0.2524526    0.4938968 4000.000 0.9995974
x_prob[20]    0.21958370    0.3541058    0.6335430 4000.000 0.9998727
x_prob[21]    0.91241451    0.9615494    0.9964914 4000.000 0.9999107
x_prob[22]    0.85743842    0.9350120    0.9944499 4000.000 0.9998915
x_prob[23]    0.12682041    0.2299418    0.4853042 4000.000 1.0002858
x_prob[24]    0.15102426    0.2611727    0.5188826 4000.000 0.9996171
z_prob[1]     0.92263662    0.9645727    0.9961818 4000.000 0.9993239
z_prob[2]     0.06412635    0.1186724    0.2634773 4000.000 0.9995061
z_prob[3]     0.14696709    0.2362540    0.4324484 4000.000 0.9992923
z_prob[4]     0.91543158    0.9591549    0.9955493 4000.000 0.9997276
z_prob[5]     0.96217694    0.9843390    0.9986652 4000.000 0.9999034
z_prob[6]     0.03690516    0.0717256    0.1881421 4000.000 1.0008297
z_prob[7]     0.07866694    0.1412252    0.2983229 4000.000 0.9998847
z_prob[8]     0.96319514    0.9854857    0.9990697 4000.000 0.9995410
lp__       -164.78851211 -161.7427068 -157.0022084 1454.294 1.0035093

全体的に分散が小さくなっていることが分かる。

事後分布

サンプル数を増やしたことで裾野が短くなっていることが分かる。
f:id:kento1109:20180705233724p:plain

トレース結果

トレース結果からも分散が小さくなっていることが分かる。
f:id:kento1109:20180705234112p:plain

さいごに

TwoCountryQuizを取り組んだが、実力不足もあり時間がかかってしまった。しかし、ラベルスイッチングやパラメータの制約に関して理解が深まったので良かった。
次はTwoCountryQuizを応用した別のタスクをを検討したい。

2018-07-11

Stan：TwoCountryQuiz①

Stan

はじめに

前回は「コワイ本」のTwentyQuestionsを取り組んだ。
kento1109.hatenablog.com

今回はそれをもう少し難しくした「TwoCountryQuiz」に取り組む。
TwentyQuestionsのコードを少し変えるだけと思っていたが、実はとても難しく嵌りどころがたくさんだった・・

それはともかく、さっそく問題を見ていく。

TwoCountryQuiz

問題の設定としては以下の通り（本文より引用）

あるグループの人々が歴史クイズを出されて、各人の各回答は正答または誤答として得点化される。人々の一部はタイ人、一部はモルドバ人である。問題の一部はタイの歴史についてのものであり、モルドバ人よりもタイ人が答えを知ってそうな問題である。残りの問題はモルドバの歴史についてのものであり、タイ人よりもモルドバ人が答えを知っていそうな問題である。
ここでは、誰がタイ人で誰がモルドバ人なのか分からず、問題の内容も分からない。データからどの人が同じ国から来た人なのか、どの問題が彼らの国と関係するのかを推定してほしい。

ちなみにモルドバ人はルーマニア語を話すラテン系の民族集団らしい。
モルドバ人 - Wikipedia

モデルの作成

ここでは2種類の回答を仮定する。
人の国籍が問題の起源と合致する場合、回答率は高い確率で正しい。（タイ人のタイの歴史の問題に対する正答率）
一方、ある人が他の国について尋ねられた場合には、回答は低い確率で正しい。（タイ人のモルドバの歴史の問題に対する正答率）
このアイデアをグラフィカルモデルにすると以下となる。

f:id:kento1109:20180704160348p:plain

この場合、 $x_i,z_j$ はそれぞれ国のインデックスを示す。
今回、 $\theta_{ij}$ は以下のように定義する。
$\theta_{ij} = \begin{cases} \alpha & (x_i=z_j) \\ \beta & (x_i\ne z_j) \end{cases}$
正答率 $\alpha$ はある人が自身の歴史の問題に対する正答率、正答率 $\beta$ はある人が他国の歴史の問題に対する正答率。仮定より $\alpha>\beta$ の制約を設ける。

離散パラメータの対応

WinBUGSの場合、このグラフィカルモデルで問題ない。ただし、そのままStanで扱うことは出来ない。パラメータ $x_i,z_j$ は（各国を示すインデックス）が離散値だからである。
離散パラメータに対応する最もシンプルな方法は「周辺化除去（marginalization ）」である。詳しくは以前に書いた。

kento1109.hatenablog.com

どう実装するべきかと調べていたら、TwoCountryQuizってどうやってStanで書くのかっていうディスカッションがあった。
groups.google.com

今回の場合は各離散パラメータの値に応じて確率分布が異なる（ $\alpha$ と $\beta$ ）ので、周辺化除去ができない。なので、パラメータ $x_i,z_j$ を確率変数として定義するのが妥当なアイデアみたいだ。 $x_i$ は $i$ 番目の人がタイ人（モルドバ人）である確率、 $z_j$ は問題 $j$ がタイ（モルドバ）の歴史に関する問題の確率を表す。
これでStanでの実装が可能となる。

モデリング

Googleでのディスカッションのアイデアに基づき以下のように実装した。

data{
  int<lower=1> nx;              // num person
  int<lower=1> nz;              // num question
  int<lower=0, upper=1> k[nx, nz];   // person * question
  real<lower=0> a;          // hyper parameter
  real<lower=0> b;           // hyper parameter
}
parameters {
  real<lower=0, upper=1> x_prob[nx];
  real<lower=0, upper=1> z_prob[nz];
  real<lower=0, upper=1> alpha;
  real<lower=0, upper=alpha> beta;
}
model {
  vector[4] lp;
  for(i in 1:nx)
    x_prob[i] ~ beta(a,b);;  // prior
  for(j in 1:nz)
    z_prob[j] ~ beta(a,b);;  // prior
  for(i in 1:nx){
    for(j in 1:nz){
      lp[1] = (log1m(x_prob[i]) + log1m(z_prob[j]) + bernoulli_lpmf(k[i, j]| alpha));
      lp[2] = (log(x_prob[i]) + log(z_prob[j]) + bernoulli_lpmf(k[i, j]| alpha));
      lp[3] = (log1m(x_prob[i]) + log(z_prob[j]) + bernoulli_lpmf(k[i, j]| beta));
      lp[4] = (log(x_prob[i]) + log1m(z_prob[j]) + bernoulli_lpmf(k[i, j]| beta));
      target += log_sum_exp(lp);
    }
  }
}

※log1m(a)は $\log (1-a)$ を効率的に計算するための関数

ポイントは尤度計算の部分。
今回は人と問題の組み合わせが２×２なので４つの式に基づき尤度が計算される。

`k[i, j]`	タイの歴史	モルドバの歴史
タイ人	`lp[1]`	`lp[3]`
モルドバ人	`lp[4]`	`lp[2]`

組み合わせの計算

なぜこのような尤度計算になるのか簡単な例で考える。

あるサイコロの出目の確率は全て「１／６」のとき、「６」が出る確率は当然「１／６」である。
次にサイコロが２つの場合を考える。
Aのサイコロの「６」が出る確率は $p_a$ であり、Bのサイコロの「６」が出る確率 $p_b$ とする。また、Aを投げる確率が $p_A$ であるとする。
このとき、「６」が出る確率は以下のような計算となる。
$\begin{eqnarray}p_A\times p_a+(1-p_A)\times p_b \end{eqnarray}$
このとき、AとBを投げる確率は排反事象であり、計算は「AまたはB」の組み合わせの確率（足し算）で求める。
これにもう一つ条件を加える。
投げ手（ホスト・ゲスト）によってサイコロの出目が変わるとする。ホストが投げる確率を $p_H$ 、サイコロと投げ手によるサイコロの「６」が出る確率は以下とする。

	ホスト	ゲスト
A	$p_{a,h}$	$p_{a,g}$
B	$p_{b,h}$	$p_{b,g}$

このとき、「６」が出る確率は以下のような計算となる。
$\begin{eqnarray}\{p_A\times p_H \times p_{a,h}\}+\{ p_A\times (1-p_H) \times p_{a,g}\} +\{ (1-p_A)\times p_H\times p_{b,h} \}+\{ (1-p_A)\times (1-p_H)\times p_{b,g}\} \end{eqnarray}$
これの対数を取ると今回のような計算になることが分かる。

推論結果

以下のようにしてデータを渡す。

尚、実験データは以下に作った。
github.com

TwoCoutryQuiz <- read.csv("TwoCountryQuiz.txt")
stan.dat <- list(nx=nrow(TwoCoutryQuiz),nz=ncol(TwoCoutryQuiz),k=TwoCoutryQuiz,a=1.0,b=1.0)
stan.fit <- stan("TwoCountryQuiz.stan",data=stan.dat)

推論結果は以下の通り。

summary(stan.fit)
$summary
                  mean     se_mean        sd          2.5%          25%         50%
x_prob[1]   0.53029713 0.036775653 0.3541604   0.011127718   0.15609154   0.5985944
x_prob[2]   0.52931333 0.037102322 0.3561591   0.010755941   0.15249905   0.5860287
x_prob[3]   0.47212875 0.030683095 0.3283253   0.011333054   0.15645041   0.4296219
x_prob[4]   0.47621507 0.025471547 0.3018463   0.019701274   0.19461178   0.4615459
x_prob[5]   0.53508411 0.037486953 0.3561731   0.013228531   0.16077255   0.6045322
x_prob[6]   0.52638124 0.031305999 0.3259938   0.022406221   0.20644299   0.5571316
x_prob[7]   0.46897241 0.033495749 0.3356998   0.015722103   0.14365877   0.4235867
x_prob[8]   0.47378394 0.030727943 0.3240059   0.013129741   0.16318500   0.4420749
z_prob[1]   0.52560515 0.031547300 0.3286305   0.018388960   0.20320846   0.5550213
z_prob[2]   0.47342530 0.032388415 0.3323511   0.010483992   0.15403045   0.4412354
z_prob[3]   0.48138335 0.024288168 0.2972166   0.021458533   0.21662389   0.4679963
z_prob[4]   0.52477091 0.030564488 0.3238213   0.021646336   0.20497649   0.5546996
z_prob[5]   0.53043538 0.037612554 0.3594749   0.009185296   0.14711397   0.5980563
z_prob[6]   0.46748793 0.036646445 0.3567124   0.008275019   0.11662093   0.4036751
z_prob[7]   0.46928308 0.031075766 0.3271401   0.012422863   0.15836508   0.4300338
z_prob[8]   0.53520960 0.036506380 0.3559883   0.011017414   0.15899693   0.6020018
alpha       0.84288128 0.004903208 0.1328105   0.495493896   0.77739007   0.8791112
beta        0.08643854 0.003764911 0.1007688   0.001575219   0.01844138   0.0486498
lp__      -76.06556122 0.129462953 3.7709042 -84.645570937 -78.28974038 -75.5811353
                  75%       97.5%     n_eff     Rhat
x_prob[1]   0.8788707   0.9907077  92.74258 1.059581
x_prob[2]   0.8841432   0.9894480  92.14802 1.062257
x_prob[3]   0.7910437   0.9855612 114.50130 1.044380
x_prob[4]   0.7592288   0.9719845 140.43037 1.040285
x_prob[5]   0.8874325   0.9919339  90.27383 1.065438
x_prob[6]   0.8409497   0.9847431 108.43353 1.052919
x_prob[7]   0.8063384   0.9830522 100.44369 1.057658
x_prob[8]   0.7888879   0.9829815 111.18311 1.049953
z_prob[1]   0.8405482   0.9845766 108.51542 1.050264
z_prob[2]   0.8033599   0.9829672 105.29670 1.055173
z_prob[3]   0.7437687   0.9731136 149.74652 1.035735
z_prob[4]   0.8337083   0.9829047 112.24744 1.046241
z_prob[5]   0.8862753   0.9926954  91.34220 1.062050
z_prob[6]   0.8405933   0.9903413  94.74860 1.060763
z_prob[7]   0.7935304   0.9819733 110.82146 1.054304
z_prob[8]   0.8860739   0.9926517  95.08980 1.058714
alpha       0.9451407   0.9944410 733.67550 1.002910
beta        0.1123582   0.3918710 716.37944 1.002677
lp__      -73.4013764 -69.9297720 848.39868 1.002594

これを見る限りRHatは問題なさそうである。
ただし、n_effが小さく見直しの余地あり。

事後分布とサンプルのトレースを確認すればモデルが良くないことが分かる。

事後分布

stan_dens(stan.fit,pars ="x_prob[1]",separate_chains = TRUE)

f:id:kento1109:20180704212745p:plain
ここから分かる問題は

明らかに分布が多峰性となっている
chainによる分布のバラつきが大きい。

ということである。
ちなみに理想的な事後分布はこんな感じ。
f:id:kento1109:20180704212849p:plain

トレース結果

stan_trace(stan.fit,pars = "x_prob[1]")

f:id:kento1109:20180704213212p:plain
理想としてはサンプリングがどこかの値付近でバラついてほしい。
しかし、取り得る範囲０～１の間を広く動いている。
（その結果、平均が0.5あたりになるのであろう。）

どう考えてもうまくいっていない・・

なぜこのような問題が起きたのか。
原因はおそらく次の２つだと考えている。

データ数の不足
ラベルスイッチング

次回、この問題に対する対処方法を考えたい。