隠れマルコフモデル（HMM）について - 機械学習・自然言語処理の勉強メモ

隠れマルコフモデル（HMM）

直前の結果のみから次の結果が確率的に求まるという「マルコフ性」を仮定して、事象をモデル化。
隠れマルコフモデル（以降HMM）では、過去の状態の遷移は不明（隠れている）な状態であり、その状態の出力結果より事象をモデル化する。

例題

下記ブログの例が分かりやすかったので、引用させて頂く。
satomacoto: 隠れマルコフモデルの例

ある友達が遠くに住んでいて、毎日何をしたかをあなたに電話で話します。友達は「散歩」「買物」「掃除」の3つのことにしか関心がありません。友達が何をするかはもっぱらその日の天気で決めます。あなたは友達が住んでいるところの天気の明確な情報は持っていません。
友人が初日に「散歩」二日目に「買い物」三日目に「掃除」という順で行動したら、その観測結果が得られる確率はいくらでしょうか、そして、このような観測結果が得られたとき三日間の天気はどのようであったでしょうか。

条件として下記の確率が与えられたとする。

start_probability （初期確率）

　　雨：0.6　晴れ：0.4

transition_probability （遷移確率）

　　雨　｛雨：0.7　晴れ：0.3｝
　　晴れ｛雨：0.4　晴れ：0.6｝

emission_probability （出力確率）

　　雨　｛散歩：0.1　買い物：0.4　掃除：0.5｝
　　晴れ｛散歩：0.6　買い物：0.3　掃除：0.1｝

与えられた初期確率、遷移確率、出力確率を用いて３日間の天気の確率を計算する。

１日目の天気

１日目	確率
☀️	0.4×0.6=0.24
☂️	0.6×0.1=0.06

２日目の天気
２日目以降は前日の状態を考慮する。

１日目	２日目	確率
☀️	☀️	0.24×(0.6×0.3)=0.0432
☀️	☂️	0.24×(0.4×0.4)=0.0384
☂️	☀️	0.06×(0.3×0.3)=0.0054
☂️	☂️	0.06×(0.7×0.4)=0.0168

３日目の天気

１日目	２日目	３日目	確率
☀️	☀️	☀️	0.0432×(0.6×0.1)=0.0026
☀️	☀️	☂️	0.0432×(0.3×0.5)=0.0065
☀️	☂️	☀️	0.0384×(0.3×0.1)=0.0012
☀️	☂️	☂️	0.0384×(0.7×0.5)=0.0134
☂️	☀️	☀️	0.0054×(0.6×0.1)=0.0003
☂️	☀️	☂️	0.0054×(0.3×0.5)=0.0008
☂️	☂️	☀️	0.0168×(0.3×0.1)=0.0005
☂️	☂️	☂️	0.0168×(0.7×0.5)=0.0059
		合計	0.0312

観測確率は起こり得る全ての事象の合計なので、0.0312
また、もっとも可能性が高い天気は「☀️→☂️→☂️」の組み合わせとなる。

上の例題の
i日目の天気を $y_i$ 、i-1日目の天気を $y_i$ 、i日目の行動を $x_i$ とすると

transition_probability： $P(y_i|y_{i-1})$
emission_probability： $P(x_i|y_i)$

と書ける。
すると、同時確率は、
$P(x,y)=\prod _{ i }{ P(x_i|y_i)P(y_i|y_{i-1}) }\cdot \cdot \cdot (1)$
と書ける。
注） $x_i$ は $y_i$ のみに依存、 $y_i$ は $y_{i-1}$ のみに依存すると仮定
（上の計算はこの同時確率の計算と同義。）

HMMの推論

自然言語処理の系列ラベリングタスクにHMMを適用する場合を考える。

例文

Mark visited Mars

に固有表現タグ

Mark	visited	Mars
NER	O	NER

がついているとする。
※簡単のためタグは固有表現（NER）かそうでないか（O)のみとする

系列ラベリングでは、文章から各単語のラベルを推定するので、

文章中の単語：観測結果（天気の問題でいう１日ごとの行動に相当）
単語のラベル：隠れ状態（天気の問題でいう１日ごとの天気に相当）

となる。
HMMでは、Viterbi アルゴリズムを使って尤もらしい経路を効率的に求めることが出来る。

Viterbi アルゴリズム

グラフの最短経路を求めるアルゴリズム。
Viterbi アルゴリズムでは、全ての結果を計算せずに前回の要素を用いて計算量を抑える。
例えば、各素性関数の重みが下記のように求まったとする。
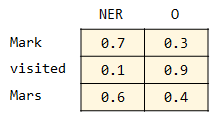
f:id:kento1109:20171213175237p:plain:w150

f:id:kento1109:20171213175237p:plain:w150

f:id:kento1109:20171213175252p:plain:w240

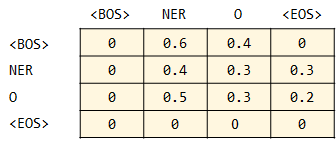
その時の最短経路（最も確率が高くなる経路）を考える。
①Mark
f:id:kento1109:20171213175732p:plain:w200

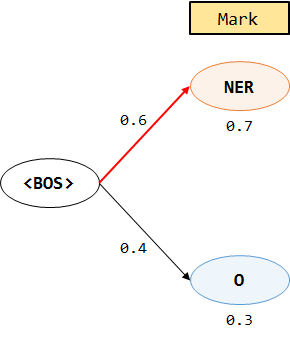
NERの確率：0.7×0.6=0.42
Oの確率：0.4×0.3=0.12
NERの確率の方が高いので、この経路を記録する。
②visited
f:id:kento1109:20171213180424p:plain:w300

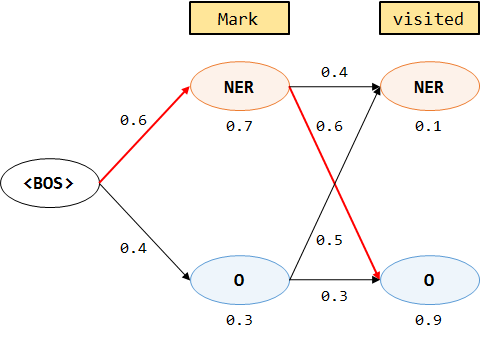
NERの確率：0.42×0.4×0.1=0.0168
Oの確率：0.42×0.6×0.9=0.2268
Oの確率の方が高いので、この経路を記録する。
③Mars
f:id:kento1109:20171213180827p:plain

NERの確率：0.2268×0.5×0.6=0.06804
Oの確率：0.2268×0.3×0.4=0.027216
NERの確率の方が高いので、この経路を記録する。
この経路（<BOS>-NER-O-NER-<EOS>）が最短経路であり、尤度最大のラベルの組み合わせとなる。

パラメータの推定

系列ラベリングの学習では、ラベル付きの訓練データが与えられる。
（学習においてラベルは隠れ状態ではない。）
系列を $x$ ,ラベル列を $y$ とした系列ラベリング問題は、

$P(y_i|y_{i-1})$
$P(x_i|y_i)$

を推定（最適化）することを目指す。

同時確率のパラメータを最尤推定により求めていく。
（ $i$ は訓練データ数）
$\begin{eqnarray}P(x^{(i)},y^{(i)})=\sum_{i}{\left( \prod _{ j }{ P(x_j^{(i)}|y_j^{(i)})P(y_j^{(i)}|y_{i-1}^{(i)}) }\right) }\cdot \cdot \cdot (2)\end{eqnarray}$

ここで、新しい変数 $\phi$ を下記のように定義する。
$\phi_{x,y}$ ： $x$ にラベル $y$ にがついている回数
$\phi_{y,y'}$ ： $y'$ の後に $y$ が現れた回数
これらの表記を用いると、(2)は下記のように書き直せる。

$\begin{eqnarray}P(x,y)=\sum_{i}{\left( \prod _{x }{\prod _{ y } {P(x|y)^{\phi_{x,y}^{(i)}}\prod _{y }{\prod _{ y' } {P(y|y')^{\phi_{y,y'}^{(i)}}} }}}\right) }\cdot \cdot \cdot (3)\end{eqnarray}$

(1)は系列の先頭から順番に各確率の掛け合わせをしていたが、(2)では各確率とその出現回数を掛け合わせている。（系列の順番を考慮する必要が無くなる。）

この対数を取ると、

$\begin{eqnarray}\log P(x,y)=\sum_{x }{\sum _{ y }(\sum_{i }{\phi_{x,y}^{(i)}) {\log P(x|y)}+\sum _{y }{\sum _{ y' }{(\sum_{i }{\phi_{y,y'}^{(i) }}){\log P(y|y')} }}}}\cdot \cdot \cdot (4)\end{eqnarray}$

また、パラメータには制約条件
$\sum_{x}{p(x|y)}=1$
$\sum_{y}{p(y|y')}=1$

が存在する。
これは、条件付き確率の総和が１になることをを保証するものである。

制約条件下でのパラメータ最大化問題なので、ラグランジュ関数は、

$\begin{eqnarray}L(\theta ,\lambda ,\mu )=\sum _{ x }{ \sum _{ y }(\sum_{i }{\phi_{x,y}^{(i)}}) { \log P(x|y)} } +\sum _{ y }{ \sum _{ y' }(\sum_{i }{\phi_{y,y'}^{(i)}}) { \log P(y|y') } } +\sum _{ y }{ \lambda _{ y }(\sum _{ x }{ p(x|y)} -1 } )+\sum _{ y' }{ { \mu }_{ y' }(\sum _{ y }{ p(y|y')} -1 } )\end{eqnarray}$
となる。
微分すると、
$\frac { \partial L }{ \partial p(x|y) } =\frac { \sum _{ i }{ \phi _{ x,y }^{ (i) } } }{ p(x|y) } +\lambda _{ y }=0 \hspace{ 0.7cm }\Rightarrow \hspace{ 0.7cm }p(x|y)=\frac { \sum _{ i }{ \phi _{ x,y }^{ (i) } } } { \lambda _{ y } }$
$\frac { \partial L }{ \partial p(y|y') } =\frac { \sum _{ i }{ \phi _{ y,y' }^{ (i) } } }{ p(y|y') } +\mu _{ y' }=0 \hspace{ 0.7cm }\Rightarrow \hspace{ 0.7cm }p(y|y')=\frac { \sum _{ i }{ \phi _{ y,y' }^{ (i) } } } { \mu _{ y' } }$

$\sum_{x}{p(x|y)}=1$
$\sum_{y}{p(y|y')}=1$
より、
$p(x|y)=\frac { \sum _{ i }{ \phi _{ x,y }^{ (i) } } } { \sum_{x}{(\sum _{ i }{ \phi _{ x,y }^{ (i) } }) }}$
$p(y|y')=\frac { \sum _{ i }{ \phi _{ y,y' }^{ (i) } } } { \sum_{y}{(\sum _{ i }{ \phi _{ y,y' }^{ (i) } } )}}$

これを求めることでモデルが作れる。

素性

パラメータ推定のための必要な情報 $\phi$ は、

$\phi _{ x,y }$ ：観測素性
$\phi _{ y,y' }$ ：遷移素性

と呼ばれ、一つの系列が一つの素性ベクトルを持つ。
例えば、先ほどの系列の前後に<BOS>、<EOS>を加えた

	Mark	visited	Mars
<BOS>	NER	O	NER	<EOS>

の場合、観測素性 $\phi _{ x,y }$ は、

$\phi _{ x,y }^{(1)}$	$x=Mark$	$y=NER$
$\phi _{ x,y }^{(2)}$	$x=visited$	$y=O$
$\phi _{ x,y }^{(3)}$	$x=Mars$	$y=NER$

であり、遷移素性 $\phi _{ y,y' }$ は、

$\phi _{ y,y' }^{(1)}$	$y=NER$	$y'=< BOS>$
$\phi _{ y,y' }^{(2)}$	$y=O$	$y'=NER$
$\phi _{ y,y' }^{(3)}$	$y=NER$	$y'=O$
$\phi _{ y,y' }^{(4)}$	$y=< EOS>$	$y'=NER$